
|
Солнечно-земная
Физика
Статьи | 
|
Динамика областей неадиабатического движения частиц в ближней магнитосфере во время суббури
Б.В. Козелов, Т.В. Козелова, (ПГИ)
в печати
Абстракт
По данным спутника CRRES оценивается геометрия областей неадиабатического движения протонов в ночном секторе ближней (5-12 RE) магнитосферы. Рассматривается динамика этих областей при переходе от подготовительной фазы к взрывной во время суббури 9 февраля 1991. Для расчётов параметра неадиабатичности была разработана и использовалась динамическая модель магнитосферы, составленная из статической модели Цыганенко-89 и магнитного поля дополнительной токовой петли, изменяющейся во времени. Параметры этой петли подбирались по наилучшему согласию с возмущениями магнитного поля, наблюдаемого на CRRES. В рамках использованной модели рассмотрены динамические изменения конфигурации магнитных силовых, проходящих через спутник CRRES и геостационарный спутник 1990-095, что позволило провести анализ изменения характера движения частиц в области проекции этих линий на экваториальную плоскость. Результаты моделирования привлекаются при обсуждении изменений в потоках частиц, наблюдаемых на спутниках. Получено, что в ночном секторе околоземной магнитосферы на расстоянии ~5-6 RE во время подготовительной фазы суббури формируется граница, разделяющая области с разным характером движения частиц. К началу суббури эта граница локально искривляется в радиальном направлении в виде выступа. Локализованная область ускорения протонов с энергиями 85-193 кэВ в начале суббури располагалась на вечерней стороне этого выступа на ~ 6.3 RE, а затем перемещалась в хвост со скоростью ~ 230 км/с.
1. Введение
Известно, что движение заряженных частиц в магнитном поле может происходить в различных режимах. При адиабатическом движении частица "привязана" к определенной силовой линии магнитного поля и в дипольном магнитном поле совершает ларморовское вращение вокруг магнитной силовой линии и колебания между зеркальными точками. При неадиабатическом движении динамика частицы может быть существенно более сложной и даже хаотичной.
В работе [Buchner and Zelenyi, 1989] было показано, что характер движения частиц в данной точке магнитосферы можно определить по значению параметра адиабатичности:
κ2 = (Rcurv /ρmax), (1)
где Rcurv - минимальный радиус кривизны магнитной силовой линии, ρmax - Ларморовский радиус частицы данной энергии с питч-углом 90o в точке с минимальным радиусом кривизны силовой линии. Областям адиабатического движения соответствует κ<1, а неадиабатическим областям - κ<<1. Переход между адиабатическим и неадиабатическим движением частицы зависит как от энергии частицы, так и от конфигурации магнитного поля, которая в свою очередь зависит от уровня магнитной активности в магнитосфере. Во время подготовительной фазы суббури, когда происходит утоньшение токового слоя и магнитные силовые линии вытягиваются в хвост магнитосферы, области хаотизации частиц приближаются к Земле на несколько Re.
Так как одно из важных следствий неадиабатического движения частиц - это сильное питч-угловое рассеяние частиц, то во многих работах положение границ областей неадиабатического движения оценивалось по положению границы изотропных распределений энергичных протонов и электронов [Imhof et al., 1977, 1979; Pytte and West, 1978; Sergeev et al.,1983; and Popielawska et al., 1985]. Область, в которой κ ~3 , была идентифицирована в работе [Sergeev et al.,1983] как экваториальная граница интенсивных высыпаний энергичных протонов (150 кэВ) в ионосферу.
В качестве меры адиабатического движения частиц, кроме параметра κ , рассматривались и другие параметры [Delcourt et al., 1994, 1996; Birmingham, 1984; Anderson et al., 1997]. Из всех параметров, используемых для систематизации режимов движения частиц в магнитосфере, только параметр δB рассмотренный в работе [Anderson et al., 1997], наилучшим образом отражает меру изменения магнитного момента частицы (см. далее формулу 3). Используя магнитосферную модель Цыганенко-89, авторы [Anderson et al., 1997] показали, что переход от адиабатического (δB~ 0.001) к неадиабатическому (δB ~ 0.1) режиму происходит в пределах ~2Re на полуночном меридиане для протонов 30 кэВ при Kp=2.
В данной работе, используя параметр δB, мы пытались проследить динамику областей неадиабатичности в околоземной магнитосфере при переходе от подготовительной к взрывной фазе конкретной суббури 9 февраля 1991 г. по данным спутника CRRES. Для расчёта δB была разработана и использовалась более реальная динамическая модель магнитосферы, составленная из статической статистической модели Цыганенко-89 и магнитного поля дополнительной токовой системы, изменяющейся во времени. Наблюдаемые на спутнике CRRES возмущения магнитного поля использовались для определения параметров этой дополнительной токовой системы.
2. Динамическая модель магнитного поля
Исследование магнитосферы Земли с помощью искусственных спутников дает обширную информацию о происходящих в ней процессах. Однако даже при наличии большого числа спутников, это всегда точечные наблюдения. Этим обусловливается необходимость привлечения магнитосферных моделей. Магнитосферная суббуря - очень динамичное явление. Поэтому при его исследовании желательно использовать динамическую модель магнитного поля. К сожалению, в настоящее время процессы, происходящие в магнитосфере Земли, исследованы не достаточно детально для построения такой модели. Существующие статистические модели (например, модели Цыганенко) не позволяют использовать их непосредственно при исследовании конкретной ситуации и требуют дополнительной адаптации.
В данной работе для исследования динамики областей неадиабатичности во время суббури в ближней (5-12 Re) магнитосфере мы разработали и использовали динамическую модель магнитосферы, составленную из статической статистической модели Цыганенко-89 [Tsyganenko, 1989] и магнитного поля дополнительной токовой системы.
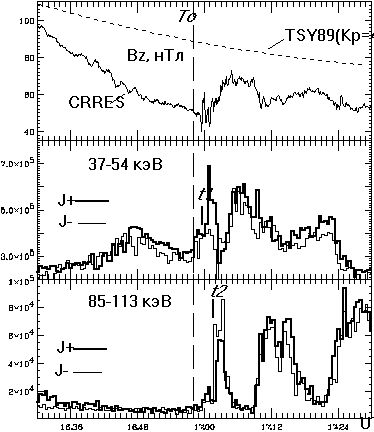
Рис.1. Суббуря 9 февраля 1991 по данным спутника CRRES, верхний график: сплошная линия - измеренная Bz компонента магнитного поля, пунктирная линия - Bz компонента, рассчитанная по модели Цыганенко-89 при Kp=4; средний график - дифференциальный поток протонов (см-2с-1ср-1кэВ-1) с энергиями 37-54 кэВ: J+ - частицы с гироцентрами ближе к Земле, чем спутник, J_ - частицы с гироцентрами дальше от Земли; нижний график - дифференциальный поток протонов с энергиями 85-113 кэВ.
Относительно дополнительной токовой системы (петли) предполагается, что она состоит из линейного тока конечной длины, лежащего в экваториальной плоскости (ZGSM=0), и линейных продольных токов, расходящихся в оба полушария на его концах. Конфигурация продольных токов рассчитывалась в предположении, что токи текут вдоль силовых линий базовой модели Цыганенко-89. Далее токи замыкаются в ионосфере. Относительно направления тока в экваториальной плоскости, его интенсивности и расстояния от Земли никаких дополнительных предположений не делалось, они подбирались для каждого момента времени таким образом, чтобы модельное магнитное поле соответствовало наблюдаемому на CRRES. Начальная длина токовой петли в экваториальной плоскости принималась равной 2Re и увеличивалась с шагом 0.4Re, если изменением других параметров не удавалось добиться достаточного согласия модельного поля с наблюдаемым. Положение середины тока по MLT для рассматриваемого далее случая (484 орбита CRRES) было фиксировано на 23.00, так как при этом интенсивности необходимых дополнительных токов оказались минимальными.
На рис.1 приведена Bz компонента магнитного поля (в GSM системе координат), измеренного на спутнике CRRES на 484-ой орбите во время суббури 9 февраля 1991. Взрывная фаза этой суббури началась в T0=16.58 UT в долготном секторе, включающем меридиан ст. Норильск и ИСЗ CRRES [Козелова и др., 1998]. На том же рисунке приведены значения Bz компоненты магнитного поля, рассчитанные вдоль траектории спутника по модели Цыганенко-89 при Kp=4. Видно, что поле в статистической модели существенно отличается от наблюдаемого и тем более не отражает динамику возмущений при переходе от подготовительной к взрывной фазе суббури.
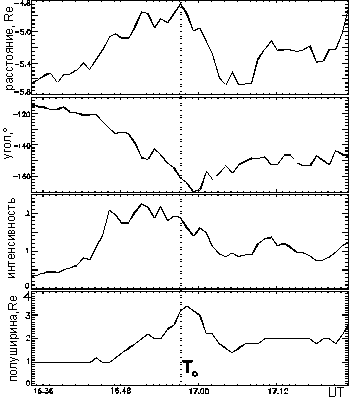
Рис.2. Параметры дополнительной токовой системы, сверху вниз: а) расстояние от Земли до середины тока в экваториальной плоскости; б) направление (угол с осью XGSM); в) интенсивность (в относительных единицах); г) длина в экваториальной плоскости.
Параметры дополнительной токовой системы, рассчитанные с шагом в 1 минуту, приведены на рис.2. Из рисунка видно:
- 1) Во время подготовительной фазы суббури дополнительный ток приближается к Земле на ~1Re, при этом его направление изменяется от почти поперечного (вечер-утро) до продольного (от Земли).
- 2) В начале рассмотренного участка подготовительной фазы происходит быстрый рост интенсивности тока (в 5 раз за 12 минут), при этом длина токовой петли в экваториальной плоскости не меняется. Однако в течение последних 12 минут перед началом взрывной фазы суббури интенсивность тока практически не меняется, но длина токовой петли в экваториальной плоскости постепенно возрастает в 3 раза.
- 3) После начала взрывной фазы суббури направления изменения всех параметров дополнительного тока меняются на обратные.
Здесь мы не обсуждаем происхождение токовой петли, отметим только, что направление тока в ней согласуется с существующими представлениями относительно распределения экваториальных токов в околоземной части плазменного слоя [Iijima et al., 1993]. Согласно [Iijima et al., 1993], радиальная составляющая токовой петли может быть обусловлена градиентами плотности плазмы в азимутальном направлении.
3. Проекции положения спутников на экваториальную плоскость
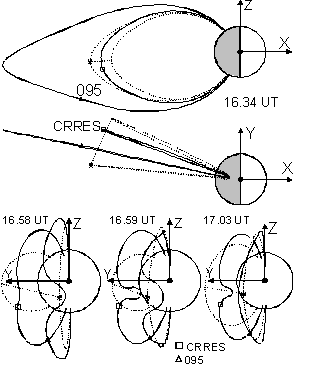 На рис.3 для нескольких моментов времени представлены примеры полученных конфигураций дополнительной токовой системы, а также показаны силовые линии магнитного поля, проходящие через спутник CRRES и геостационарный спутник 1990-095 и рассчитанные с учетом этих дополнительных токов.
На рис.3 для нескольких моментов времени представлены примеры полученных конфигураций дополнительной токовой системы, а также показаны силовые линии магнитного поля, проходящие через спутник CRRES и геостационарный спутник 1990-095 и рассчитанные с учетом этих дополнительных токов.
Рис.3. Примеры конфигураций дополнительной токовой системы и силовых линий, проходящих через спутник CRRES и геостационарный спутник 1990-095.
Из этого рисунка видно, что несмотря на близость этих спутников в пространстве, силовые линии, проходящие через них, сильно отличаются по своей форме и пересекают экваториальную плоскость на разных расстояниях. Кроме того, радиальная составляющая дополнительного тока приводит к существенному искривлению магнитных силовых линий в азимутальном направлении (на восток) вблизи начала суббури.
Наиболее важной точкой для определения характера движения частиц на данной силовой линии является вершина магнитной силовой линии, так как в этой точке обычно минимален радиус кривизны силовой линии (Rcurv). Координаты (расстояние от Земли и MLT) вершин силовых линий, проходящих через спутники CRRES и 1990-095, для рассматриваемого события приведены на рис.4.
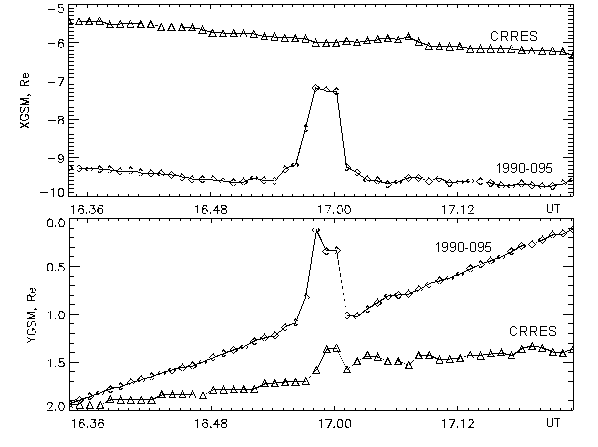
Рис.4. Сравнение положений проекций вершин силовых линий, проходящих через спутники CRRES и 1990-095, во время окончания подготовительной и начала взрывной фаз суббури 9 февраля 1991.
Видно, что в начале подготовительной фазы суббури вершины силовых линий медленно отодвигаются от Земли, т.е. происходит медленное вытягивание силовых линий в хвост магнитосферы. Однако затем, за 3-4 минуты до Тo, наблюдается некоторый сбой и в связи с разворотом токовой петли в радиальном направлении расстояние до вершины силовой линии, проходящей через геостационар 1990-095, резко уменьшается на 2 Re и возвращается обратно через ~3 мин после начала взрывной фазы. Для силовой линии, проходящей через CRRES, изменения незначительны (~0.1 Re). По MLT положение вершин силовых линий для обоих спутников смещается ближе к полуночи за ~2 мин до начала взрывной фазы и возвращается обратно через ~3 мин после начала взрывной фазы.
4. Области неадиабатического движения частиц
Для более детального анализа изменения характера движения энергичных частиц во время суббури вблизи спутников CRRES и 1990-095 будем использовать параметр δB, рассчитываемый по формуле [Anderson et al., 1997]:
 (2)
Здесь: α - питч-угол частицы на экваторе, ε = (ρmax/Rcurv )= 1/κ2 , , функция F определена как:
(2)
Здесь: α - питч-угол частицы на экваторе, ε = (ρmax/Rcurv )= 1/κ2 , , функция F определена как:
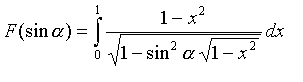 В отличие от параметра κ , см. формулу (1), в параметре δB учитывается зависимость от питч-угла. Кроме того, параметр δB имеет простой физический смысл, так как связан с изменением первого адиабатического инварианта частицы за одно пересечение экваториальной плоскости:
В отличие от параметра κ , см. формулу (1), в параметре δB учитывается зависимость от питч-угла. Кроме того, параметр δB имеет простой физический смысл, так как связан с изменением первого адиабатического инварианта частицы за одно пересечение экваториальной плоскости:
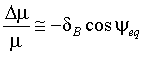 (3)
(3)
Здесь m= mv_
2/2B - первый адиабатический инвариант частицы с массой m в магнитном поле напряженностью B, v_ - перпендикулярная полю компонента скорости частицы; ψeq - гирофаза частицы при пересечении экваториальной плоскости. Здесь ψeq = 0, когда мгновенная скорость частицы при её гировращении направлена вдоль оси X, а фаза ψeq = 90° соответствует скорости частицы в направлении на утро в ночном секторе магнитосферы.
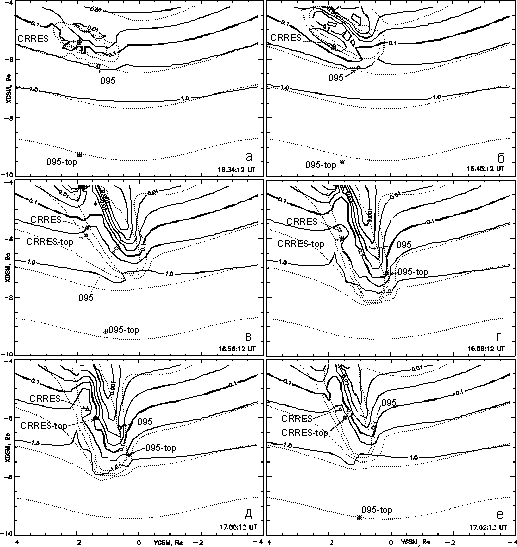
Рис.5. Геометрия областей неадиабатического движения частиц в ночном секторе ближней (5-12 Re) магнитосферы. Сплошные линии - изолинии значений параметра неадиабатичности δB для протонов с энергией 150 кэВ и экваториальным питч-углом >αeq=45о; пунктирные линии - изолинии B=const. CRRES и 095 - положение спутников в проекции на экваториальную плоскость, CRRES-top и 095-top - положение вершин силовых линий, проходящих через спутники.
Примеры рассчитанных линий постоянных δB для протонов с энергиями E = 150 кэВ и питч-углом на экваторе α=45о в ночном секторе экваториальной плоскости магнитосферы приведены на рис.5 для нескольких характерных моментов времени рассматриваемого события. Видно, как по мере развития дополнительного тока во время подготовительной фазы суббури вблизи этого тока возникает область с резким переходом от адиабатического (δB<0.01) к неадиабатическому (δB>0.1) движению. Минимальная ширина этой переходной области порядка 0.5 Re. Разворот дополнительной токовой петли вблизи Тo приводит к искривлению контуров равного δB в радиальном направлении в виде выступа. С утренней стороны от этого выступа область адиабатического движения заходит в виде узкой полосы, вытягивающейся в направлении от Земли в хвост. С вечерней стороны от выступа располагается сильно неадиабатическая область. Переходная область на рис. 5 является некоторым аналогом границы, разделяющей разные режимы движения частиц, определённые по параметру κ, которую авторы Ashour-Abdalla et al. [1992] назвали "стенкой" ("wall"). Авторы Ashour-Abdalla et al. [1992] для расчётов использовали модель Цыганенко-89 и "стенка" у них имеет ориентацию "утро-вечер". Однако из рис. 5 видно, что в более реальной динамической модели магнитного поля, которую мы используем, "стенка" локально искривляется в том секторе, где затем происходит суббуревая интенсификация.
Рассматриваемые изменения μ обусловлены исключительно геометрией магнитного поля и соотношением кривизны силовой линии с гирорадиусом частицы в околоэкваториальном слое, где радиус кривизны минимальный. Выйдя из этого слоя и перемещаясь к зеркальной точке и обратно, частица одновременно дрейфует по долготе и затем снова пересекает этот слой в точке, где значения δB могут быть другими. Когда частица быстро дрейфует в область меньшего δB из области сильного изменения μ, значение <μ для нее может быть "заморожено" на большем значении, чем первоначальное, и частица может соскочить с одной дрейфовой оболочки на другую. На рис.5 штриховыми линиями показаны линии равного B. Около начала суббури изолинии B поля, как и контуры δB , изгибаются и в наиболее удалённой от Земли в хвост части заходят в сильно неадиабатичную область, где δB > 1, т.е. где возможно предельное изменение dμ ~ μ даже за одно пересечение области рассеяния. Для частиц, дрейфующих по изолиниям B, такое соскакивание на другую дрейфовую оболочку возможно на вечерней стороне изгиба изолиний. Как будет видно дальше из следующего раздела, именно по эту сторону изгиба видны первые возрастания потоков протонов вблизи начала суббури.

Рис.6. Значения параметра δB вблизи вершины силовой линии, проходящей через спутник CRRES. Положение вершины силовой линии показано звездочками.
Изолинии параметра δB , вычисленные для протонов других энергией и питч-углов, в общих чертах, повторяют динамические свойства изолиний для 150 кэВ, изображённых на рис.5. Изменения параметра δB для протонов с энергией 45 кэВ (центральная энергия в канале P1 на спутнике CRRES) вблизи вершины силовой линии, проходящей через спутник CRRES, представлены на рис.6 в зависимости от времени и от MLT. Видно, что характер движения частиц в непосредственной близости от спутника изменяется наиболее сильно при переходе от подготовительной к взрывной фазе суббури.
5. Изменения в потоках частиц
Анализ потоков частиц и магнитного поля на спутнике CRRES во время суббури 9 февраля 1991 г. приводился в работах [Козелова и др., 1998, Lazutin et al, 1998]. Как отмечалось в [Козелова и др., 1998], поведение магнитного поля на CRRES около Тo = 16.58 UT отражало, по крайней мере, два процесса. Один процесс - это колебания типа Pi2 и второй - более медленные изменения магнитного поля в виде вытягиваний силовых линий или их диполизации. Кроме того, было отмечено, что вблизи начала суббури потоки протонов менялись некогерентно на расстояниях порядка 2ρi и имели противоположную азимутальную анизотропию в разных энергетических каналах. Области ускорения протонов, с которыми связаны последовательные возрастания потоков частиц (активизации), изменяли своё положение относительно ИСЗ, располагаясь со временем дальше от Земли.
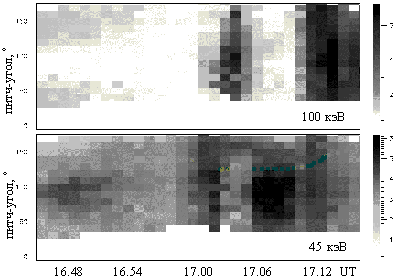
Рис.7. Питч-угловое распределение протонов в двух каналах во время суббури 9 февраля 1991 по данным спутника CRRES. Шкала справа - значения десятичного логарифма от дифференциального потока частиц.
На рис. 7 приведены питч-угловые распределения протонов в каналах Р1 и Р4. Видно, что инжекции протонов в этих каналах начинаются в разные моменты времени и имеют разные распределения по питч-углам. Остановимся на связи динамики наблюдаемых потоков частиц с изменениями в характере их движения.
В рассмотренном случае вплоть до 16.45 UT силовая линия, проходящая через CRRES, находится в более адиабатической области. В этом промежутке времени питч-угловое распределение низкоэнергичных (канал P1) протонов имеет максимум на 90o (колоколообразное или захваченное распределение), а для более энергичных, а значит менее адиабатичных, протонов (каналы P4-P5) - максимум смещен от 90o (Рис. 7). Плавное возрастание потоков протонов Р1 на подготовительной фазе суббури начинается в 16.43 UT (за 15 мин до Т0) [Козелова и др., 1998]. С этого времени до Тo, более неадиабатичная область приближается к Земле (панели 'б' и 'в' на рис. 5) и питч-угловое распределение протонов в канале P1 становится изотропным (Рис. 7).
В интервале 1658-1701 UT силовая линия, проходящая через CRRES, сдвигается на восток и ее вершина опять оказывается в более адиабатической области (панели 'г' и 'д' на рис.5). Именно в это время наблюдается начало первого суббуревого возрастания потоков протонов Р1-Р3 почти без дисперсии, причём потоки J+ больше потоков J_, т.е. источник частиц находится ближе к Земле, чем ИСЗ [Козелова и др., 1998]. Питч-угловое распределение меняется с изотропного на захваченное (Рис. 7). Магнитное поле вытягивается и некоторое время продолжает оставаться таким, осциллируя с периодом около 50 с [Козелова и др., 1998].
В момент 17.01 UT наблюдается второе возрастание потоков протонов, которое захватывает более энергичные частицы в каналах Р4-Р6, причём J_>J+ [Козелова и др., 1998]. В это время силовая линия, проходящая через CRRES, возвращается обратно и оказывается в более неадиабатической области. Таким образом, прослеживается связь между наблюдаемыми свойствами инжекций частиц и характером движения частиц. А именно, возрастаниям менее энергичных частиц с J+>J_ соответствует переход к более адиабатическому движению, а возрастаниям более энергичных частиц с J_>J+ - переход к более неадиабатическому движению.
Как видно из рис. 5, в ходе суббури вершина силовой линии, проходящей через геостационарный ИСЗ 1990-095, оказывается то в более, то в менее адиабатичных областях, как и для CRRES. Однако в потоках частиц на ИСЗ 1990-095 имелись две особенности. Первая особенность - это "квазивыход" спутника в доли хвоста, который длился 2 минуты, начиная с 17.00 UT [Thomsen et al., 1994]. Напомним, что в это время спутник CRRES видит первую после начала суббури инжекцию менее энергичных протонов. Как видно из рис. 5 (панель "д"), в это время проекции обоих спутников на экваториальную плоскость оказываются вблизи токовой петли, но по разные стороны от неё. Разное поведение частиц на этих двух спутниках может свидетельствовать о локальности области источника частиц в начале суббури. Вторая особенность - запаздывание инжекции энергичных протонов на ИСЗ 1990-095 на 1 минуту относительно начала инжекции более энергичных частиц на CRRES. К началу инжекции силовая линия, проходящая через ИСЗ 1990-095, опять вытягивается в хвост (панель "е" на рис. 5). Учитывая положение вершин силовых линий, проходящих через CRRES и 1990-095, и временную задержку, можно сказать, что область ускорения частиц в начале суббури локализована, что первоначальное положение этой области было на ~ 6.3 Re (около CRRES), а затем она перемещалась в хвост со скоростью ~ 230 км/с.
Таким образом, результаты моделирования магнитного поля, приведенные в предыдущих разделах, показывают, что последовательные инжекции частиц с разными свойствами соответствуют на экваториальной плоскости областям с разным характером движения, чем можно объяснить разное поведение потоков частиц на двух близких спутниках около начала суббури.
6. Обсуждение
Ускорение частиц во время диполизации магнитного поля в взрывную фазу суббури представляет особый интерес. Ещё Pellinen and Heikkila [1978] подчёркивали огромную роль индукционного электрического поля в ускорении протонов вплоть до энергий в несколько МэВ. Они полагали, что процесс энергизации частиц состоит из двух шагов (two-step behavior): неадиабатического возрастания магнитного момента и адиабатического ускорения. Mauk [1986] воспроизвёл импульсное ускорение во время диполизации и получил дисперсионные зависимости для инжекций частиц с энергиями < 20 кэВ, похожие на наблюдаемые на геостационарной орбите. В работе Delcourt, Sauvaud, 1994] [было показано, что включение неадиабатических эффектов приводит к значительно большему, чем получалось у Mauk [1986], ускорению частиц. Авторы работ [Borovsky et al., 1981; Birmingham, 1984] в качестве механизма энергизации частиц предлагали известный общий механизм ускорения заряженных частиц - магнитную накачку [Альвен, Фельтхаммар, 1967]. Механизм магнитной накачки является следствием комбинированного действия адиабатического процесса (бетатронного ускорения) и процессов рассеяния, которые приводят к изменению адиабатических инвариантов. Этот механизм особенно эффективен в областях, где ожидается неадиабатическое поведение частиц из-за их питч-углового рассеяния.
Наши вычисления показывают,что такой механизм накачки может действовать во время взрывной фазы суббури. Действительно, как видно из рисунков, к началу суббури 9 февраля 1991 г. внутренняя граница области с неадиабатическим характером движения частиц располагается на r~ 5-6 Re и потоки протонов с энергиями 85-193 кэВ (в каналах Р4-Р6), ускоренных во время взрывной фазы суббури, наблюдаются в области сильной неадиабатичности, которым соответствуют большие значения δB. В этой области на экваториальной плоскости из-за геометрии магнитного поля и соотношения минимальной кривизны силовой линии с гирорадиусом частицы происходит кратковременное нарушение адиабатической инвариантности и магнитный момент частиц μ испытывает значительные флуктуации, максимальное значение которых составляет dμ ~ μ [Anderson et al., 1997]. Во время диполизации электрическое поле, связанное с (dB/dt), будет вызывать ускорение частиц, наиболее эффективное именно в этой сильно неадиадиабатической области с большим питч-угловым рассеянием. Внутренняя граница этой неадиабатической области может иметь смысл границы инжекции частиц. В конкретной ситуации механизм накачки будет неэффективен для частиц с более низкими энергиями, для которых рассеяние более слабое. Это может объяснить отсутствие возрастания потоков протонов с энергиями 37-69 кэВ одновременно с инжекцией более энергичных >85 кэВ протонов [Lazutin et al., 1998].
Кроме того, результаты проведенного выше анализа позволяют продвинуться в понимании ещё одного общего вопроса, связанного с магнитосферной динамикой, а именно в понимании зависимости L оболочки изотропной границы от энергии. По наблюдениям на низковысотных спутниках [Popielowska et al, 1985] достаточно часто при изменении L переход от захваченного питч-углового распределения к изотропному распределению для частиц данной энергии происходит очень быстро. Такие наблюдения трудно объяснить, используя только статистическую статическую модель магнитного поля. Приведенные выше расчеты с использованием более реалистической модели магнитного поля показывают, что области чисто адиабатического и сильно неадиабатического движения частиц могут находиться достаточно близко, на расстояниях Dx ~ 1Re , для протонов в широком диапазоне энергий. Тем самым находит объяснение наблюдаемый быстрый переход от захваченного питч-углового распределения, соответствующего частицам в адиабатической области, к изотропному, характерному для области неадиабатического рассеяния.
7. Выводы
Для анализа динамики областей неадиабатичности во время суббури в ближней (5-12 Re) магнитосфере мы разработали и использовали динамическую модель магнитосферы, составленную из статической статистической модели Цыганенко-89 [Tsyganenko, 1989] и магнитного поля дополнительной токовой системы. Наблюдаемые на спутнике CRRES возмущения магнитного поля использовались для определения параметров этой дополнительной токовой системы. Результаты расчетов с использованием динамической модели магнитосферы показывают следующее:
- 1) Во время суббури искривление силовых линий происходит не только в радиальном, но и в азимутальном направлении. Это приводит к тому, что перед началом суббури даже сравнительно близко расположенные спутники проектируются в экваториальной плоскости на значительные расстояния друг от друга и могут попадать в разные области магнитосферы. Такое искажение магнитных силовых линий может объяснить разное поведение потоков частиц на этих спутниках около начала суббури.
- 2) В ночном секторе околоземной магнитосферы на расстоянии ~ 5-6 Re во время подготовительной фазы суббури формируется граница, разделяющая области с разным характером движения частиц, определённым по параметру δB. К началу суббури эта граница локально искривляется в радиальном направлении в виде выступа таким образом, что к Земле и на утро от выступа - движение адиабатическое, а в хвост и на вечер - неадиабатическое. На вечерней стороне выступа во время наибольшей его деформации затем происходит суббуревая активизация.
- 3) Возрастаниям менее энергичных частиц с J+>J_ соответствует переход к более адиабатическому движению, а возрастаниям более энергичных частиц с J_>J+ - переход к более неадиабатическому движению.
- 4) Локализованная область ускорения частиц первоначально располагалась на ~ 6.3 Re, вблизи сравнительной резкой границы, разделяющей области с разным характером движения частиц, а затем она перемещалась в хвост со скоростью ~ 230 км/с.
Благодарности. Работа выполнена при поддержке Российского фонда фундаментальных исследований, грант РФФИ №01-05-64827.
Список литературы
Альвен Г., Фельтхаммар К.-Г. Космическая электродинамика // М.,Мир, 1967. 260c.
Козелова Т.В., Лазутин Л.Л., Козелов Б.В., Расинкангас Р., Корт А., Зингер Г. Динамика возрастаний потоков протонов во время суббури по наблюдениям на спутнику CRRES // Геомагнетизм и аэрономия. Т.38. №1. С.74-86. 1998.
Anderson B.J., Decker R.B., Paschalidis N.P. Onset of nonadiabatic particle motion in the near-Earth magnetotail // J. Geophys. Res. V. 102. № A8. P.17533-17569. 1997.
Ashour-Abdalla M., Zelenyi L.M., Bosqued J.M., Peroomian V., Wang Z., Schriver D., Richard R. Effects of near-Earth stochastic acceleration and reflections of magnetotail ions on the formation of auroral arcs // Proceedings of the First International Conference on Substorms. Kiruna, Sweeden, 23-27 March, 1992. P. 545-552. 1992.
Birmingham T.J. Pitch angle diffusion in the Jovian magnetodisc // J. Geophys. Res. V.89. №A5. P.2699-2707. 1984.
Borovsky J.E., Goertz C.K., Joyce G. Magnetic pumping of particles in the outer Jovian magnetosphere // J. Geophys. Res. V.86. №A5. P.3481-3495. 1981.
Buchner J., Zelenyi L.M. Regular and chaotic charged particle motion in magnetotaillike field reversals. 1.Basic theory of trapped motion// J.Geophys.Res. V.94, №A9. P.11821-11842. 1989.
Delcourt D.C., Sauvaud J.-A., Martin R.F., Jr., Moore T.E. On the nonadiabatic precipitation of ions from the near-Earth plasma sheet // J. Geophys. Res. V.101. №8. P.17409-17418. 1996.
Delcourt D.C., Martin R.F., Jr., Alem F. A simple model of magnetic moment scattering in a field reversal // Geophys.Res.Lett. V. 21. №14. P.1543-1546. 1994.
Iijima T., Watanabe M., Potemra T.A., Zanetti L.J., Kan J.R., Akasofu S.-I. Substorm currents in the equatorial magnetotail // J.Geophys.Res. V.98. №10. P.17283-17298. 1993.
Imhof W.L., Reagan J.B., Gaines E.E. Studies of sharply defined L dependent energy threshold for isotropy at the midnigth trapping boundary // J. Geophys. Res. V.84. №A11. P.6371-6384. 1979.
Imhof W.L., Reagan J.B., Gaines E.E. Fine-scale structure in the pitch angle distributions of energetic particles near the trapping boundary // J. Geophys. Res. V. 82. №32. P.5215-5221. 1977.
Lazutin L.L., Rasinkangas R., Kozelova T.V., Korth A., Singer H., Reeves G., Riedler W., Torkar K., Gvozdevsky B.B. Observations of substorm fine structure // Ann. Geophysicae. V.16. №7. P.775-786. 1998.
Mauk B. H. Quantitative modeling of the "convection surge" mechanism of ion acceleration // J. Geophys. Res. V. 91. № A12. P.13423-13431. 1986.
Pellinen R.J., Heikkila W.J. Energization of charged particles to high energies by an induced substorm electric field within the magnetotail // J. Geophys. Res. V.83 №A4. P.1544-1550. 1978.
Popielawska B., Szalinska-Piechota E., Tsyganenko N.A. On the non-adiabatic particle scattering in the Earth's magnetotail current sheet // Planet. Space Sci. V. 33. №12. P.1433-1437. 1985.
Pytte T., West H.T., Jr. Ground-satellite correlations during pre-substorm magnetic field configuration changes and plasma thinning in the near-Earth magnetotail // J. Geophys. Res. V.83, №8. P. 3791-3804. 1978.
Sergeev V. A., Sazhina E.M., Tsyganenko N. A., Lundblad J. A., Soraas F. Pitch-angle scattering of energetic protons in the magnetotail current sheet as the dominant source of their isotropic precipitation into the nightside ionosphere // Planet. Space Sci. V.31. №10. P.1147-1155. 1983.
Thomsen M.F., Bame S.J., McComas D.J., Moldwin M.B., Moore K.R. The magnetospheric lobe at geosynchronous orbit // J. Geophys. Res. V.99. №A9. P.17283-17293. 1994.
Tsyganenko N.A. A magnetospheric magnetic field model with a warped tail current sheet // Planet. Space Sci. V. 37. №1. P.5-20. 1989.
Переход на другие страницы проекта "СиЗиФ"
Для связи:
[email protected]
последнее обновление 5.04.03






 На рис.3 для нескольких моментов времени представлены примеры полученных конфигураций дополнительной токовой системы, а также показаны силовые линии магнитного поля, проходящие через спутник CRRES и геостационарный спутник 1990-095 и рассчитанные с учетом этих дополнительных токов.
На рис.3 для нескольких моментов времени представлены примеры полученных конфигураций дополнительной токовой системы, а также показаны силовые линии магнитного поля, проходящие через спутник CRRES и геостационарный спутник 1990-095 и рассчитанные с учетом этих дополнительных токов. 
 (2)
(2)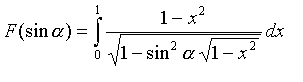
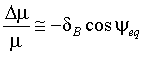 (3)
(3)






